In this tutorial, I will explain the working of differential equations and how to solve a differential equation. At the start a brief and comprehensive introduction to differential equations is provided and along with the introduction a small talk about solving the differential equations is also provided. After that a brief introduction and the use of the integral block present in the simulink library browser is provided and how it can help to solve the differential equation is also discussed. After that an example is performed in which a second order differential equation is solved on simulink along with the description of each step and the use and working of each block. At the end a simple exercise is provided regarding the concepts and blocks used in this tutorial.
How to solve differential equations in simulink
- In simulink library browser, as we have seen in previous tutorial there is a block named as Integral as shown in the figure below,
Figure 1: Integration
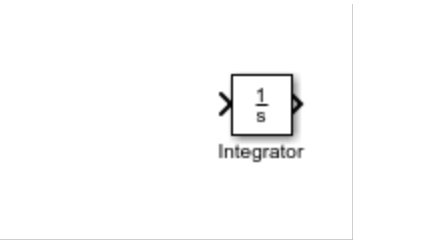
- As the name suggests, this block is used to calculate the integral of the signal provided at the input i.e. left side of the block. In case of solving a differential equation, the major this we have to do is to integrate the given equation which will return the function without the derivative as is obvious from the equation below,
- Integration of the derivative of a function is equal to the function itself. The purpose of the integral block here is the same. Number of integral blocks used in a block diagram is equal to the order of the differential equation we are going to solve hereby in the problem. For instance, if we want to solve a 1st order differential equation we will be needing 1 integral block and if the equation is a 2nd order differential equation the number of blocks used is two. Lets’ now do a simple example using simulink in which we will solve a second order differential equation.
Block diagram of differential equations in Simulink
- Lets’ open MATLAB first to start working with Simulink as we have done in the previous tutorial. Open the simulink by either typing simulink in the command window or using the Simulink icon. On the simulink start page click on the library browser icon to open the library browser as shown in the figure below,
Figure 2: Library browser
- In the simulink library browser a large number of blocks are present. Click on the most commonly used sub block as shown in the figure below,
Figure 3: Commonly used blocks
- We will be writing a simulink program or in simple words we will create a block diagram that will solve the differential equation given below. The first step to be done here is to rearrange the differential equation. On the left hand side write the highest order derivative and move all the remaining terms on the right hand side as given in the equation below,
- From the library browser, select the commonly used blocks and then select integral block as shown in the figure below,
Figure 4: Integral block
- Drag and drop the integral block on the simulink blank project created previously. Also save the project so we can use it sometime later as we have done in previous tutorials. If we are working with a second order differential equation we will place two integral blocks as shown in the figure below,
Figure 5: Second order integral
- And if we are working with third order differential equation we will be using three integral blocks as shown in the figure below,
Figure 6: 3rd order integral
- In our case, however, the number of blocks to be used is 2 as the order of differential equation is 2. To provide the co-efficient present with each equation i.e. the 4 with we will use a gain block as shown in the figure below,
Figure 7: Gain block
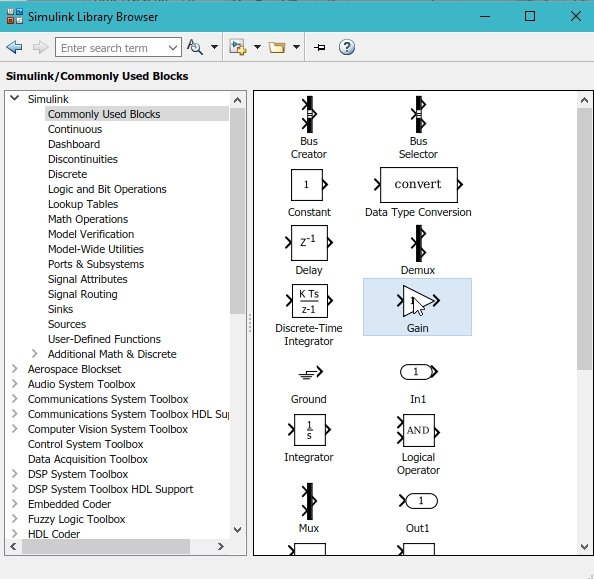
- We will need two gain blocks, the second will be used to multiple 5 with the . Also to place the 1 present at the right hand side of the given equation, we will need a constant block as shown in the figure below,
Figure 8: Constant block
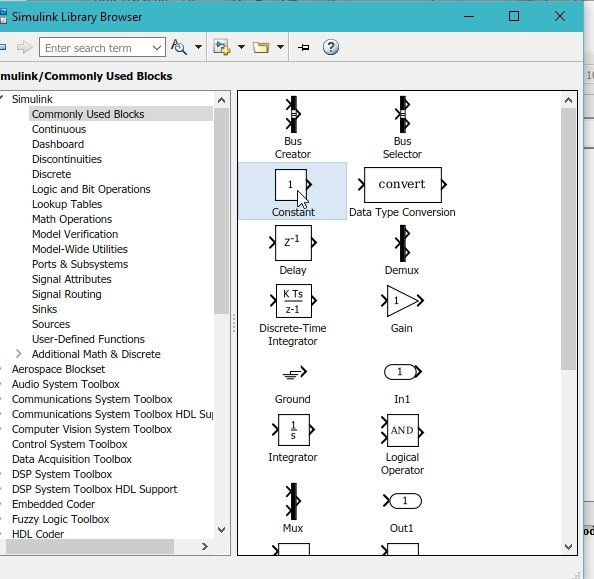
- And to add all the terms on the right hand side of the rearranges equation we will use a summation block as shown in the figure below,
Figure 9: Sum block
- Place all the components as shown in the figure below, before jumping to the connecting portion,
Figure 10: Placed components
- As we want to first multiply the term and then add it hence we should flip the gain block. This can be done by right clicking on the block then select Rotate & Flip and then select Flip block as shown in the figure below,
Figure 11: Flipping block
- Double click on the gain block and change the gain of the block as shown in the figure below,
Figure 12: Changing gain
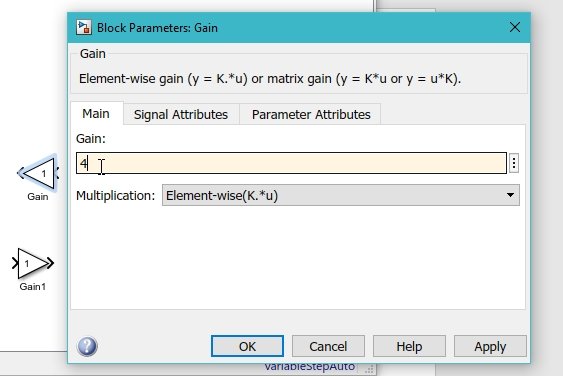
- Do the same with the other gain block and change its gain to 5 as shown in the figure below,
Figure 13: Gain blocks
- Next comes the summation block. Double click on the summation block. We can also change the shape of the summation block from round to rectangle in the block parameters dialog box of sum as shown in the figure below,
Figure 14: Shape of sum block
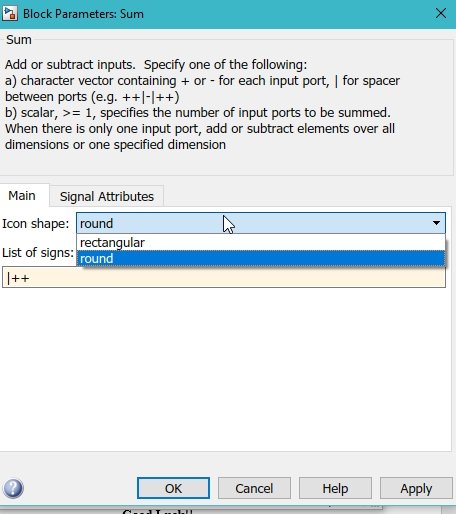
- We can also change the number of terms to be added here by changing the sequence of list of signs in the parameters of the block, and also change them from sum to subtract as shown in the figure below,
Figure 15: List of signs
- This list is adjusted according to the right hand side of the rearranged equation. After than connect the constant to the + side of the sum block as shown in the figure below,
Figure 16: Constant
- Connect all the integration blocks together and label them accordingly to perform all the derivative iterations as shown in the figure below,
Figure 17: Derivation steps
- Now, Connect the wire labeled as with the gain block 4 and connect the output of the gain block to the negative sign of the sum block as shown in the figure below,
Figure 18: Second term
- Lets’ now evaluate the third term i.e. . Connect the wire labeled as y to the input of the gain block with gain 5 and connect its output to the only left slot in sum block as shown in the figure below,
Figure 19: Third term
- From the library browser select an oscilloscope from the commonly used blocks, named as Scope as shown in the figure below,
Figure 20: Scope
- Connect it at the output i.e. at the end of the wire labeled as y. The complete block diagram to perform the solution of the differential equation is shown in the figure below,
Figure 21: Complete block diagram
- Run the block diagram from the Run icon as shown in the figure below,
Figure 22: Running the block diagram
- After the simulation is complete double click on the scope and the waveform of the equation is displayed as shown in the figure below,
Figure 23: Output
Exercise:
- Perform the above discussed problem on a third order differential equation. Use the equation given below and solve it on simulink.
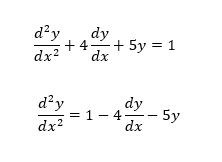
Please I would like To Built Digital Video Broadcast Using Auduino, For Transmitting and Receiving Like Now Days Digital Decorders, Now Will i Able to communicate with Arduino to work as Decorder?
Please if yes please i failed its commanding Language.
(d^2 y)/(dt^2 )= dy/dt+y^2+3 with the initial conditions y(0)=1,(dy/dt)_0=-1
Using SIMULINK obtain the profiles of y(t),dy/dt, and (d^2 y)/(dt^2 ) over a simulated time period of 20 secs.
Hello Monika, you can choose the initial values in the properties of the integral block. Double click the block and see the tab that says “initial value”. That simple
hi! thank you for this post, it helps me a looooot!
I have a question. I have u(t) instead of constant 1 on this post, then what should I use instead of constant?
and also I have yy’, instead of 4y , 4y’, or something like that… is there any way to solve this one?
so I get y”+y’+yy’+4y=u(t)
thank you for your help again!
This was very helpful, really appreciated. Thanks for the good work