Auto intensity control of street lights using pic microcontroller

Auto intensity control of street lights using  pic microcontroller, In this article you will learn how auto intensity control system of street lights works? How to control auto intensity of street lights? What is the purpose of auto intensity control of street lights? How you can design this project very easily using simple electronic components and pic16f877a microcontroller. Let’s start with basic introduction of auto intensity control of street lights.

Auto intensity control of street lights :

 Basic purpose of this project is to make street lights intelligent so that it can turn it on and off itself. Another feature of this project is that street lights intensity vary according to intensity of light and number of vehicles on road. Followings are the main features of this project :

1. Street lights turns itself on automatically during night or darkness. They turn themself off automatically during day time and during visible intensity of light.
2. Street lights controls its intensity automatically according to intensity of light. For example in evening intensity of light start decreasing at the same time street lights start increasing its intensity. When there is no intensity of light in after evening, street lights turn themself on with full intensity till midnight at 12:00 am.
3. There is another feature included in this project that is vehicle detection. Infrared sensor circuit is used to detect vehicles on road. After 12:00am street lights start decreasing their intensity. At 1:00am street lights turn off automatically. After 1:00 am function of vehicle detection starts. If there is any vehicle on road after 1:00am, street lights turns on for 2 minutes. After that they turn off automatically. In other words, After 1:00am street lights turn on only if there is any vehicle on road. Otherwise they remain off. This process remains till morning. But after having visible intensity of light during moring street lights turn off automatically.

Advantages of auto intensity control of  street lights :

As it name suggest suggests it makes use of street lights very easy. Some of the main advantages of them are given below:

• No need to control street lights manually.
• Electrical power saving.
• Increases life time of street lights.
• intelligent street lights.
• vehicle detection.

Circuit diagram description :

Followings are the main components of auto intensity control of street lights. I have explained all these components and their functions briefly.

DS1307 real time clcok:

DS1307 real time clock is use to keep information of time during day and night. Time is used to control intensity of light and its turn on and turn off ability after 12:00 am. So real time clock ds1307 is interfaced with pic microcontroler to keep information of real time.

Light dependent resistor ( LDR) :

Light dependent resistor is a kind of light sensor which is used to measure intensity of light. LDR is interfaced with pic16f877a microcontroller to measure intensity of light. This measured intensity of light is used to control street lights and their intensity.

Infrared sensor :

Infrared sensor is a combination of infrared transmitter and receiver. This is used  for detection of vehicles after 1:00 am. If there is any vehicle on road after 1:00am, street lights turns on automatically for 2 minutes otherwise remain off. I have already explained the main function of infrared sensor circuit for this project.

Light crystal display :

LCD ( liquid crystal display ) is used to display time and status of street lights. If street lights are on, LCD will display street lights are on, otherwise it display street lights are off.

Circuit diagram of auto intensity control of street lights:

complete circuit diagram of auto intensity control of street lights is given below :

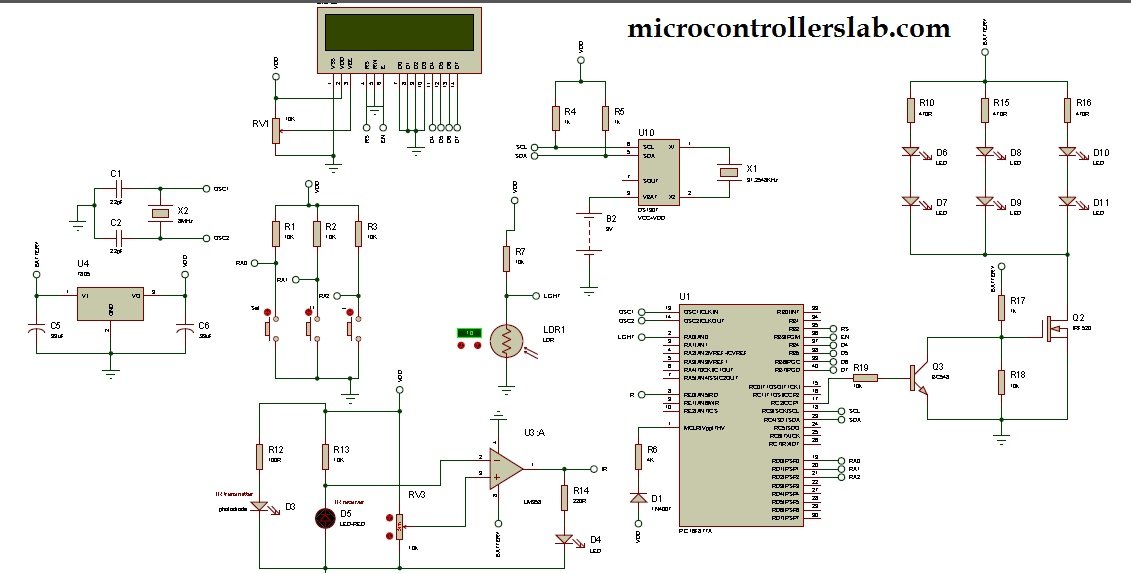
I have already explained this circuit diagram above, But if you still have any issue about it, you can wrie in comments.

List of components  for auto intensity control of street lights:

Category,Reference,Value,Order Code
Resistors,"R1",10K,
Resistors,"R2",10K,
Resistors,"R3",10K,
Resistors,"R7",10k,
Resistors,"R18",10k,
Resistors,"R19",10k,
Resistors,"R4",1k,
Resistors,"R5",1k,
Resistors,"R8",1k,
Resistors,"R17",1k,
Resistors,"R6",4K,
Resistors,"R10",470R,
Resistors,"R15",470R,
Resistors,"R16",470R,
Capacitors,"C1",22pF,Digikey 478-1018-6-ND
Capacitors,"C2",22pF,Digikey 478-1018-6-ND
Integrated Circuits,"U1",PIC16F877A,
Integrated Circuits,"U10",DS1307,
Transistors,"Q2",IRF520,
Transistors,"Q3",BC548,
Diodes,"D1",1N4007,
Diodes,"D6",LED,
Diodes,"D7",LED,
Diodes,"D8",LED,
Diodes,"D9",LED,
Diodes,"D10",LED,
Diodes,"D11",LED,
Miscellaneous,"B2",3V,
Miscellaneous,"LCD2",LM016L,
Miscellaneous,"LDR1",TORCH_LDR,
Miscellaneous,"RV1",10K,Digikey 3005P-101-ND
Miscellaneous,"X1",31.2548KHz,
Miscellaneous,"X2",8MHz,

Code for auto intensity control of street lights:

Code for this project is written in Mikro C for pic. Complete C code for auto intensity control of street lights is given below :

[sociallocker]// LCD module connections
sbit LCD_RS at RB2_bit;
sbit LCD_EN at RB3_bit;
sbit LCD_D4 at RB4_bit;
sbit LCD_D5 at RB5_bit;
sbit LCD_D6 at RB6_bit;
sbit LCD_D7 at RB7_bit;

sbit LCD_RS_Direction at TRISB2_bit;
sbit LCD_EN_Direction at TRISB3_bit;
sbit LCD_D4_Direction at TRISB4_bit;
sbit LCD_D5_Direction at TRISB5_bit;
sbit LCD_D6_Direction at TRISB6_bit;
sbit LCD_D7_Direction at TRISB7_bit;
// End LCD module connections

unsigned short read_ds1307(unsigned short address)
{
unsigned short r_data;
I2C1_Start();
I2C1_Wr(0xD0); //address 0x68 followed by direction bit (0 for write, 1 for read) 0x68 followed by 0 –> 0xD0
I2C1_Wr(address);
I2C1_Repeated_Start();
I2C1_Wr(0xD1); //0x68 followed by 1 –> 0xD1
r_data=I2C1_Rd(0);
I2C1_Stop();
return(r_data);
}

void write_ds1307(unsigned short address,unsigned short w_data)
{
I2C1_Start(); // issue I2C start signal
//address 0x68 followed by direction bit (0 for write, 1 for read) 0x68 followed by 0 –> 0xD0
I2C1_Wr(0xD0); // send byte via I2C (device address + W)
I2C1_Wr(address); // send byte (address of DS1307 location)
I2C1_Wr(w_data); // send data (data to be written)
I2C1_Stop(); // issue I2C stop signal
}

unsigned char BCD2UpperCh(unsigned char bcd)

{
return ((bcd >> 4) + ‘0’);
}

unsigned char BCD2LowerCh(unsigned char bcd)
{
return ((bcd & 0x0F) + ‘0’);
}

int Binary2BCD(int a)
{
int t1, t2;
t1 = a%10;
t1 = t1 & 0x0F;
a = a/10;
t2 = a%10;
t2 = 0x0F & t2;
t2 = t2 << 4;
t2 = 0xF0 & t2;
t1 = t1 | t2;
return t1;
}

int BCD2Binary(int a)
{
int r,t;
t = a & 0x0F;
r = t;
a = 0xF0 & a;
t = a >> 4;
t = 0x0F & t;
r = t*10 + r;
return r;
}

int second;
int minute;
int hour;
int hr;
int ap;
int light;
int pwm;
int ir;
int adc_value = 0;

unsigned short set_count = 0;
short set;

char time[] = “00:00:00 PM”;
void main()
{
I2C1_Init(100000); //DS1307 I2C is running at 100KHz
TRISD = 0x07;
PORTD = 0x00;
TRISE.F0 = 1;
TRISC.F2 = 0; // designate PORTC pins as output
PORTC.F2 = 0; // set PORTC to 0

Adc_Init();
Lcd_Init();
PWM1_Init(5000);
PWM1_Start(); // start PWM1 // Initialize LCD
Lcd_Cmd(_LCD_CLEAR); // Clear display
Lcd_Cmd(_LCD_CURSOR_OFF); // Cursor off
Lcd_out(1,1,”Time:”);
do
{

set = 0;

if(PORTD.F0 == 0)
{
Delay_ms(100);
if(PORTD.F0 == 0)
{
set_count++;
if(set_count >= 4)
{
set_count = 0;
}
}
}
if(set_count)
{
if(PORTD.F1 == 0)
{
Delay_ms(100);
if(PORTD.F1 == 0)
set = 1;
}

if(PORTD.F2 == 0)
{
Delay_ms(100);
if(PORTA.F2 == 0)
set = -1;
}
if(set_count && set)
{
switch(set_count)
{
case 1:
hour = BCD2Binary(hour);
hour = hour + set;
hour = Binary2BCD(hour);
if((hour & 0x1F) >= 0x13)
{
hour = hour & 0b11100001;
hour = hour ^ 0x20;
}
else if((hour & 0x1F) <= 0x00)
{
hour = hour | 0b00010010;
hour = hour ^ 0x20;
}
write_ds1307(2, hour); //write hour
break;
case 2:
minute = BCD2Binary(minute);
minute = minute + set;
if(minute >= 60)
minute = 0;
if(minute < 0)
minute = 59;
minute = Binary2BCD(minute);
write_ds1307(1, minute); //write min
break;
case 3:
if(abs(set))
write_ds1307(0,0×00); //Reset second to 0 sec. and start Oscillator
break;

}
}
}

second = read_ds1307(0);
minute = read_ds1307(1);
hour = read_ds1307(2);
hr = hour & 0b00011111;
ap = hour & 0b00100000;
time[0] = BCD2UpperCh(hr);
time[1] = BCD2LowerCh(hr);
time[3] = BCD2UpperCh(minute);
time[4] = BCD2LowerCh(minute);
time[6] = BCD2UpperCh(second);
time[7] = BCD2LowerCh(second);
if(ap)
{
time[9] = ‘P’;
time[10] = ‘M’;
}
else
{
time[9] = ‘A’;
time[10] = ‘M’;

[button-brown url=”http://store.microcontrollerslab.com/product/auto-intensity-control-of-street-lights-using-pic-microcontroller/” target=”_self” position=”center”]Click here to purchase code, circuit diagram and proteus simualtion[/button-brown]

Note: This code is not complete. you can purchase complete code from me in 50$. But I recommend you to write your own code but if you can’t write, you can purchase from me. This all effort is from my side. Kindly share this article with your friends and social media. That’s what you can do for me in retrun. Thanks 🙂