In this tutorial, we will discuss the linear equation and its simulation using Simulink. For this, we will design a block diagram that will help us solve a system of linear equations. At the start, we provide a brief introduction to linear equations and systems of linear equations. After that, we will perform a simple example on MATLAB Simulink in which a sample system of linear equations is taken and we solve for the variables with the help of Simulink. The example requires us to solve two linear equations for two unknowns; we can, however, extend it to solve a larger number of equations simultaneously. At the end, a simple exercise is provided regarding the concepts and blocks used in this tutorial.
Introduction to Linear Equations and Systems of Linear Equations
A linear equation is a mathematical term that is in the form of unknown variables whose power is one and which can be written in the form of a point-slope equation as given below.
y = mx + c
Here m is the slope of the line and c is the y-intercept. The graph of a linear equation is a straight line. A system of linear equations is, however, a set of linear equations that contain the same variable. The number of equations is equal to the number of unknowns present in the equation. For instance, if the system contains 5 linear equations, then the number of unknowns or variables in all these equations collectively is also 5, with each equation satisfying the definition of a linear equation (having the power of each variable equal to 1). In this tutorial, we are going to solve a system of linear equations with two equations and two unknowns. The equations are given below.
2x + 3y = -4
4x + 5y = -5
Let’s suppose the general system was
a1*x + b1 * y = -k1
a2*x + b2 * y = -k2
This implies that a1 = 2, b1 = 3, k1 = 4, a2 = 4, b2 = 5, and k2 = 5.
We will use these values later in this tutorial.
How to Solve Linear Equations with Simulink
Let’s move towards a simple example for solving a system of linear equations using Simulink. In Simulink, a block named Algebraic Constraint will help us by doing the job. However, it is not that simple; we also have to apply some logic in order to solve the system of linear equations.
Now we will begin with the programming part. Open MATLAB and then Simulink, as we did in previous tutorials. After that, open the library browser and select the commonly used blocks. From that section, select the gain block. Now drag and drop that gain block onto the Simulink block diagram section. Place two such gain blocks, as the example we have taken here is for two unknown variables, as shown in the figure below.
These gain blocks are used to enter the value of the coefficient of each of the variables; hence, the number of gain blocks is equal to the number of unknowns in the equation. As we are using a system of equations with two unknowns, the number of gain blocks is two.
Next comes the constant part. The constant on the right-hand side of the equation can be placed as a constant block. From the commonly used blocks section in the library browser of Simulink, select the block of a constant and place it with the two already placed gain blocks, as shown in the figure below.

Math Operations
Now what we need to do is add all three blocks. To do so, we can also use the sum block, but as we are interested in exploring more blocks in Simulink, we will use another block provided by Simulink to add things together. From the library browser, click on the Math Operations section, as shown in the figure below.

From this section, select the add block as shown in the figure below.

This add block will do the same job as the sum block we have used in previous tutorials. As we can see, the number of inputs provided by this add block is two; however, we want to add up three things together (two gain blocks and one constant), so we now need to update the parameters of the add block. Double-click on the add block, and in the list of signs, add a + sign to increase the number of inputs, as shown in the figure below.
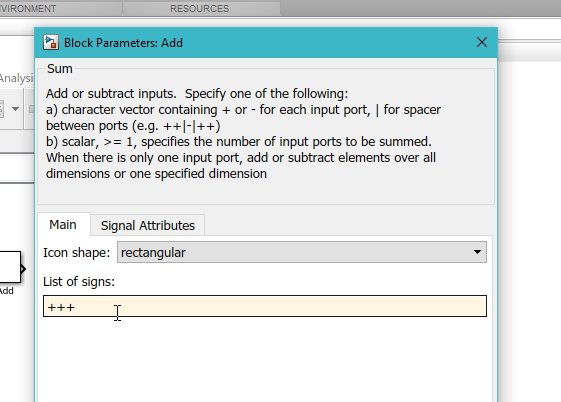
At the input of the add block, connect all the already placed blocks, i.e., two gain blocks and a constant, with the help of a wire, as shown in the figure below.
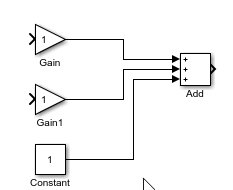
Algebraic Constraints
This is the adder of equation 1, so we will name the gain and constant as a1, b1, and k1. The next step here is to place an Algebraic Constraint block. This constraint block inputs a function whose input should be equal to zero and estimates the output of the function’s value. The output of the block must be provided to the input coefficient through a feedback loop, and with each iteration, the output value will be updated until we receive a correct value for that unknown. The initial value provided to the constraint block is zero here. From the math operations section, select the Algebraic Constraints block as shown in the figure below.
At the input of that block, connect the output of the adder. Now select the sinks section from the library browser of Simulink, as shown in the figure below.
From this section, select the display block as shown in the figure below.
Simulink Model
Place this block at the output of the constraint block. This block is used to display the output of the program. We have now designed a complete block diagram of one of the equations, as shown in the figure below.

Simply copy and paste this complete block diagram to get the block diagram of the second equation, as shown in the figure below.
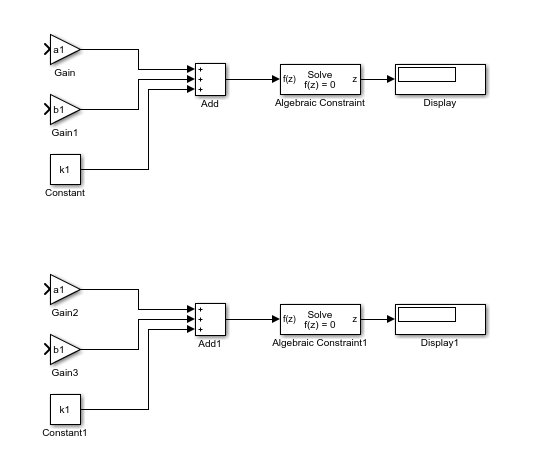
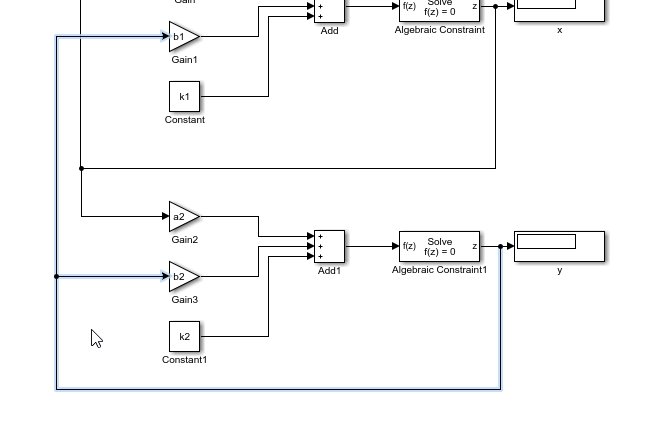
Hence, here we update the variable names of the second block to a2, b2, and k2. Now comes the part of connecting the feedback to the constraint block. Firstly, we will connect the feedback wire from the output of the 1st constraint block to the input of blocks a1 and a2, as these are the coefficients of x (which will be displayed in the 1st constraint block), as shown in the figure below.

Do the same with 2nd constraint block and b1, b2, as shown in the figure below.
Command Window
The highlighted wires show the feedback path for the y value. Now go back to the MATLAB command window, where we will define the values of the variables as shown in the figure below.

So, here we define all the values of the variables in the command window as we have given in the introduction portion, as shown in the figure below.

Simulation
After we run the command, these variables will appear in the workspace of MATLAB, which can also be accessed in Simulink, as shown in the figure below.
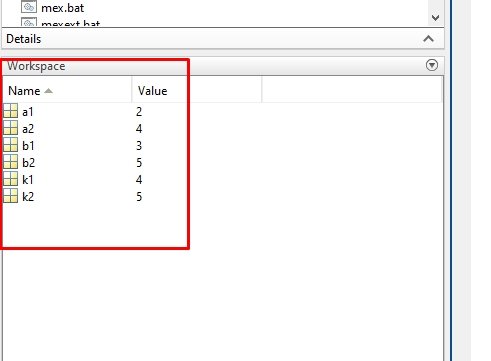
At last, we run the Simulink block diagram from the run icon on the screen, and the output of the solution of the system of linear equations will be displayed in the display box as shown in the figure given below.

Exercise
- Design a block diagram that will be able to solve three linear equations with three unknowns as provided in the equations given below.
3x+4y-2z=9 ; 5x+2y+z=0 ; x-y+5z=11
Conclusion
In conclusion, this tutorial provides an in-depth overview of solving linear equations using Simulink. It covers step-by-step procedures along with an example with explanations to help us better understand the concept. You can utilize these concepts to solve more complex problems with linear equations. At last, we have provided an exercise to reinforce the concept of this tutorial. Hopefully, this was helpful in expanding your knowledge of designing and simulating using Simulink.
You may also like to read:
- Raspberry Pi Pico W Send Sensor Readings to ThingSpeak (BME280)
- Raspberry Pi Pico DHT22 Web Server (Weather Station)
- VHDL programming if else statements and loops with examples
- Arduino Watchdog Timer Tutorial with Example
- 74LS83 4-Bit Full Adder
- Half Adder and Full Adder Simulation using PSpice: Tutorial 13
This concludes today’s article. If you face any issues or difficulties, let us know in the comment section below.


