FIR Filter Design in Simulink Guide

In this tutorial, we will discuss filters, their uses, and their benefits. At the start, we provide a brief and general introduction to filters. Then we will discuss Finite Impulse Response (FIR) filters. After that, we provide an explanation of the different orders of FIR filters. Using the information provided in the introduction, a simple and comprehensive FIR filter of second order is designed in the subsection “Explanation with Example”. In this subsection, we provide a step-by-step explanation along with the results of the filter. At the end, a simple and easy-to-perform exercise is provided for the reader to do on their own related to the concept provided in the tutorial.

Introduction to Filters

Filters are a very basic component used by almost every single electrical engineer. As the name suggests, a filter is used to filter out unwanted or noisy components and features from the input. In general, the filters can take any input, but when we talk about signal processing specifically, the input must be an electrical signal. Now, redefining the filter, it is a process of removing unwanted components or noise from an input signal. There are various types of signals, but we will only discuss a few of them here.

Types of Filters

Filters can be classified into the following types:

FIR Filters (Finite Impulse Response)	IIR Filters (infinite impulse response filter)
High-pass and Low-pass Filters	Band-pass Filters
Stop-band Filters	Notch Filters
Comb Filters	All-pass Filters

To name a few but we will only discuss FIR filters here.

FIR Filters

A finite impulse response filter (FIR filter) can easily be understood by its name. It provides a finite-length output response to an input impulse. In simple words, FIR filters give a finite-duration output in response to an impulse, as we will see shortly in the example below. Coming over to the order of FIR filters, it is defined as the order of their transfer function. For an Nth-order FIR filter, the output is only dependent on the first N input samples. We will design a second-order FIR filter in this tutorial. A general design of a FIR filter is shown in the figure below.

FIR Filter Design in Simulink Matlab — FIR filter design

Designing FIR Filters in Simulink

Now let’s design a second-order FIR filter. A comparison of an equation with its general form is done below. So, to find the coefficients b₀, b₁, and b₂, we will write them as follows: the general form on the left side and its corresponding coefficient on the right side.

b₀= 2, b₁ = 1, b₂= 2

Placing Components

Now, let’s design this filter in MATLAB’s Simulink. First of all, open MATLAB and then Simulink, as we have been doing in previous tutorials. Create a blank model to design a simple FIR filter. Open the library browser of Simulink, and from the commonly used blocks, select the constant block as shown in the figure below. This block will serve as the coefficient of the equation.

Delay Block

Next, we will need a delay block, which will serve as the x[n-1] and x[n-2] delayed samples. The order of the filter will determine the number of delay blocks to be used in the filter design. In our example, the order of filters is 2, hence the number of delay blocks. From the commonly used blocks section, select the delay block and place it on the model as shown in the figure below.

Sum Block

The number of stages of an FIR filter to be designed will also depend on the order of the filter. If the order of the filter is N, then the number of stages to be used in the filter design will be N+1. In our case, the order of the filter is 2, and hence the stages will be 3. At the end of the filter stages, we will have to sum up the output of all the stages, as is obvious from the equation of our system. For this summation process, we have to use a sum block. From the Math Operation section in the Simulink library browser, select the sum block and add it to the model as shown in the figure below.

Product Block

Also, in order to multiply the coefficient of each stage with the delayed input, we have to use some product blocks. In the library browser, from the section of Math Operations, select the Product block and place it in the model as shown in the figure below.

Input Source

The next step is to add some input sources in order to see the correct response of the system. The input source we will use here is Repeating Sequence Stairs. The purpose of using this block is to generate an impulse, as we will see shortly. From the sources section of the library browser of Simulink, select the Repeating Sequence Stairs block and add it to the model as shown in the figure below.

Scope

In order to display the output of the filter, we also need some kind of oscilloscope to display input along with output. From the sinks section of the library browser, select scope and add it to the model as shown in the figure below.

Now let’s move to the model we created at the start to jump towards the designing part of the filter. As we have discussed previously, our filter will have three stages. We will design each stage step by step. First of all, place the input source on the left and double-click on it to change its input to an impulse. In the parameter block, add the sequence of inputs as shown below.

Stages of FIR Filter

Now, using the equation given for the filter, we will start designing from left to right. The first part of the equation will be the first stage, as shown in the figure below.

The same input will then be used with a single delay to make the second stage and multiplied by the constant value of 1, as shown in the figure below.

Second stage of FIR filter — Second stage

The same will happen in the case of the third stage with one more delay block at the output of the first delay block to provide the twice delayed input, i.e., x[n-2], as shown in the figure below.

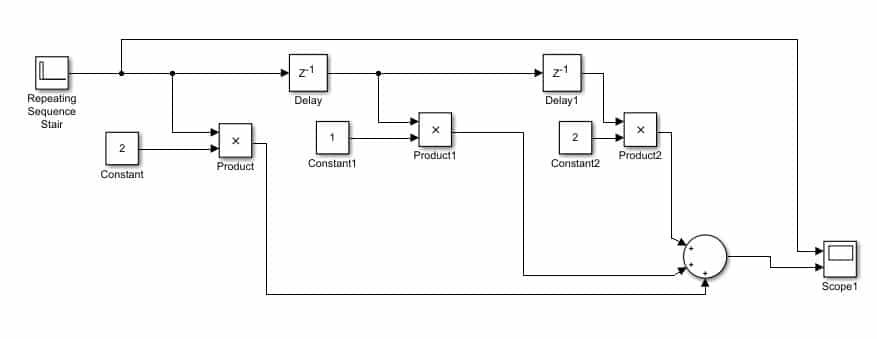
Complete Block Diagram

Now we will add the output of all three stages using the sum block. But first, change the number of inputs in the sum block, as we have done previously. And at the output of the sum block, connect a scope with two inputs (one for the input and one for the output), as shown in the figure below.

Simulation

Now change the simulation stop time to 1, as we have done before, and run the Simulink model. After the completion of the run, double-click on the scope, and the output of the filter will look like the one shown in the figure below.

The output of the filter is in accordance with the explanation in the introduction.

Exercise

Design a third order FIR filter of the system given in the equation below.
(Hint: Number of delay blocks to be used will be 3)

Conclusion

In conclusion, this tutorial provides an in-depth overview of designing and simulating FIR filter in Simulink. It covers step-by-step procedures along with explanation of an example to helps us better understand the concept. You can utilize this concept to design various other types of filters in Simulink. At the end, we have provided an exercise to reinforce the concept of this tutorial. Hopefully, this was helpful in expanding your knowledge of Simulink.