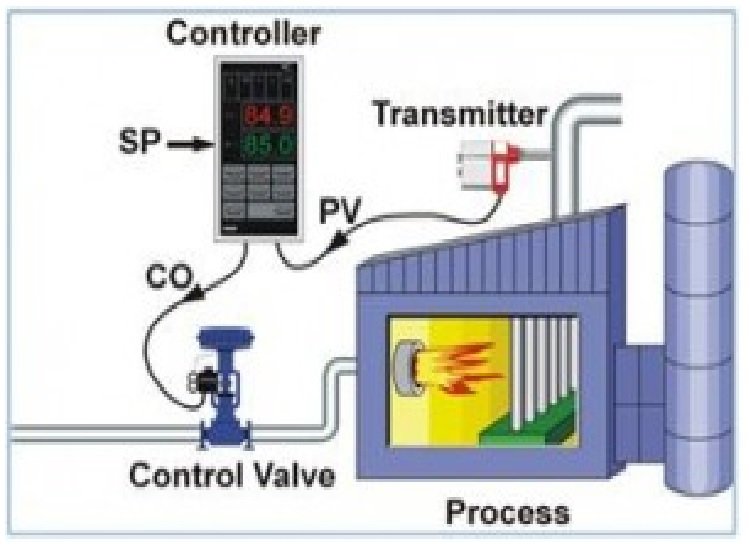
PID Controller Working and Tuning Types

In this article, we will discuss the PID controller. PID controller stands for proportional-integral-derivative controller (PID controller or three-term controller). It is a control circle input instrument, which we generally utilize as a part of modern control frameworks. It is an assortment of different applications requiring consistently regulated control. A PID controller ceaselessly ascertains a blunder or incentive as the distinction between a coveted setpoint (SP) and a deliberate procedure variable (PV) and applies a revision in view of relative, fundamental, and subsidiary terms (meant P, I, and D individually) which give the controller its name.

In reasonable terms, it consequently applies an exact and responsive revision to a control work. An ordinary illustration is the journey control on a street vehicle. Where outside impacts, for example, slopes, would cause speed changes, and the driver could adjust the coveted set speed. The PID calculation reestablishes the genuine speed to the coveted speed in the ideal route, immediately or overshoot, by controlling the power yield of the vehicle’s motor.

The primary hypothetical examination and commonsense application were in the field of programmed directing frameworks for ships, created from the mid-1920s onwards. It was then utilized for programmed process control in the assembling industry, where it was broadly actualized in pneumatic and, after that, electronic controllers. Today, there is all-inclusive utilization of the PID idea in applications requiring exact and enhanced programmed control.

PID Controller Structure

A PID controller comprises three terms: specifically corresponding, necessary, and subsidiary control. The consolidatory task of these three controllers is to provide control techniques for process control. The PID controller controls the procedure factors like weight, speed, temperature, stream, and so forth. A portion of the applications utilize PID controllers. In some cases, we need to utilize at least two PIDs to accomplish control.

The above figure shows the structure of PID controllers. It comprises a PID piece, which gives its yield to the process square. The process or plant comprises conclusive control gadgets like actuators, control valves, and other control gadgets to control different procedures in the industry or plant. Input motion from the procedure plant is contrasted, and a set point or reference flag u(t) and a related blunder flag e(t) are added to the PID calculation. As indicated by the relative, basic, and subordinate control figures in the calculation, the controller produces a consolidatory reaction or control yield that connects to plant control gadgets. All control applications don’t need to bother with all three control components. Blends like PI and PD controls are frequently utilized as part of viable applications.

Working of PID Controller

With the utilization of an easy, straightforward ON-OFF controller, just two control states are conceivable: completely ON or completely OFF. Its utilization is for restriction control applications where these two control states are sufficient for the control objective. However, the swaying nature of this control confines its use, and consequently, it is being supplanted by PID controllers. The PID controller keeps up the yield with the end goal that there is zero mistake between the process variable and the set point or desired yield by shut-circle tasks. PID utilizes three fundamental control practices that are clarified underneath.

P- Controller

The corresponding P-controller gives yield, which is relative to the current mistake e(t). It contrasts wanted or set points with genuine esteem or input process esteem. The subsequent blunder duplicates itself with relative consistency to get the yield. On the off chance that the blunder esteem is zero, at that point this controller yield is zero. This controller requires biasing or manual reset when utilized alone. This is on account of the fact that it never achieves the consistent state condition. It gives stable activity, but dependably keeps up the relentless state blunder. The speed of the reaction is expanded when the relative steady Kc increments.

I-Controller

Because of the impediment of the p-controller, where there dependably exists a balance between the procedure variable and set point. We require the I-controller, which provides an important activity to dispose of the enduring state error. It coordinates the mistake over some undefined time frame until the point when blunder esteem compasses to zero. It holds the incentive for a conclusive control gadget, at which a blunder ends up zero. Vital control diminishes its yield when a negative blunder happens. It confines the speed of reaction and influences the strength of the framework. The speed of the reaction is expanded by diminishing indispensable pick-up Ki.

In the above figure, as the gain of the I-controller diminishes, the unfaltering state blunder additionally continues diminishing. In the vast majority of cases, the utilization of a PI controller is necessary, especially where there is no requirement for a rapid reaction.

While utilizing the PI controller, I-controller yield is restricted to some degree to beat the necessary breeze-up conditions. Where indispensable yield continues expanding even at the zero mistake state because of nonlinearities in the plant.

D-Controller

The I-controller doesn’t have the ability to foresee the future consequences of a mistake. So it responds ordinarily once the set point changes. D-controller defeats this issue by expecting future conduct of the mistake. Its yield relies upon the rate of progress of the blunder regarding time, duplicated by subsidiary steady. It gives the kickstart for the yield along these lines, expanding the framework reaction.

In the above figure, the reaction of the D controller is greater in comparison with the PI controller. Furthermore, the settling time of yield is diminished. It enhances the dependability of the framework by compensating stage slack caused by the I-controller. Expanding the subordinate pick-up builds speed of reaction.

So at long last, we saw that by joining these three controllers, we can get the coveted reaction for the framework. Distinctiveness outlines diverse PID calculations.

Tuning Techniques for PID Controller

Prior to the working of the PID controller, it requires tuning to suit the progression of the procedure we need to control. Architects give the default esteems for P, I, and D terms, and these qualities couldn’t give the coveted execution and now and again prompt precariousness and moderate control exhibitions. There are diverse kinds of tuning techniques for PID controllers that require much consideration. The administrator needs to choose the best estimations of corresponding, necessary, and subordinate additions. Some of these are given below.

Trial and Error Method

It is a basic strategy for PID controller tuning. While the framework or controller is working, we can tune the controller. In this technique, first we need to set Ki and Kd esteems to zero and increment the relative term (Kp) until the point that the framework ranges to wavering conduct. When it is wavering, change Ki (Integral term) with the goal that motion stops, and lastly, modify D to get a quick reaction.

Process reaction curve technique

It is an open-circle tuning strategy. It produces a reaction when a stage input is connected to the framework. At first, we need to apply some control yield to the framework physically and record the reaction bend. After that, we have to ascertain the incline, dead time, and rise time of the bend, and then substitute these qualities in P, I, and D conditions to get the gain estimations of PID terms.

Zeigler-Nichols method

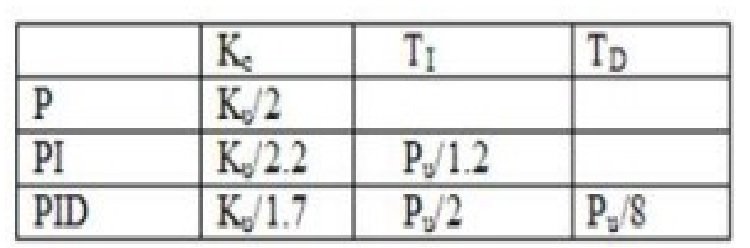
Zeigler-Nichols proposed closed-circuit strategies for tuning the PID controller. Those are constant cycling technique and damped wavering strategy. The techniques for the two strategies are the same, yet swaying conduct is extraordinary. In this, first we need to set the p-controller steady and Kp to a specific esteem, while Ki and Kd esteems are zero. Relative pick-up expands until the framework wavers toward consistent adequacy. The pick-up at which the framework produces steady motions is called extreme pick-up (Ku), and the time of motions is called extreme period (Pc). When it achieves this, we can enter the estimations of P, I, and D in the PID controller by Zeigler-Nichols table depending on the controller utilized, like P, PI, or PID, as demonstrated as follows:

Applications of PID Controllers

PID controllers have various applications in industrial automation, robotics, environmental control systems and automotive industry.

Industrial Automation

PID controllers have many uses in industrial automation to control various processes such as temperature, pressure, flow, level, and speed. These provide accurate and precise control to ensure that the process variable stays close to the desired setpoint. The utilization of PID controllers is found in manufacturing plants, refineries, chemical industries, and power plants.

Robotics and Motion Control

These controllers are essential components in robotics and motion control systems. They maintain stability, accuracy, and smoothness of motion in robotic arms, drones, CNC machines, and many other automated systems. The PID controllers can regulate the position, velocity, or torque of the motor, ensuring precise control in these applications by adjusting the control gains.

Environmental Control Systems

PID controllers are crucial to maintaining optimal conditions in environmental control systems. HVAC systems, greenhouses, incubators, and climate control systems rely on PID controllers for the regulation of temperature, humidity, and other environmental variables. PID controllers ensure a comfortable and controlled environment by continuously monitoring the process variable and adjusting the control output.

Automotive Industry

There are various applications of PID controllers in the automotive industry. One of the prominent examples is the engine control unit (ECU) in vehicles, which utilizes PID controllers for the regulation of fuel injection, air-fuel mixture, and idle speed. Their applications also include other systems such as cruise control systems, anti-lock braking systems (ABS), and suspension control systems, enhancing safety and performance on the road.

Conclusion

In conclusion, this article provides an in-depth overview of PID controllers. It covers their basic introduction, structure, working, types of tunings and lastly the applications. This helps us in better understanding the concept of PID controllers. Hopefully, this was helpful in expanding your knowledge.